백준 단계별 25 그래프와 순회
7562 Knight Moves
1697 Catch That Cow
2178 미로 탐색
1012 유기농 배추
2667 단지번호붙이기
1260 DFS와 BFS
Codeforces #805 Div. 3
https://codeforces.com/contest/1702
Dashboard - Codeforces Round #805 (Div. 3) - Codeforces
codeforces.com
결과

언제쯤 4/7의 벽을 통과할까.
A번
주어진 수보다 작은 10^k 중 k의 최댓값을 찾으면 되는 문제다.
void solve(){ int m; cin>>m; int value = 1000000000; vector<int> rounds; while(value >= 1){ rounds.push_back(value); value /= 10; } for(int v : rounds){ if(m - v < 0) continue; else{ cout<<m - v<<'\n'; return; } } }
B번
simulation 문제. set size가 3보다 작거나, 3인 상황에서 set에 중복된 것이 있다면 insert하고 idx++해주는 간단한 문제.,
void solve(){ string str; cin>>str; int days = 0, idx = 0, len = str.length(); while(1){ set<char> s; while(1){ if(s.size() < 3 || s.find(str[idx]) != s.end()){ s.insert(str[idx]); } else{ break; } idx++; if(idx >= len){ break; } } days++; if(idx >= len) break; } cout<<days<<'\n'; }
C번
풀이와 내 풀이는 거의 유사하지만... 내 풀이처럼 map의 value에 vector를 넣고, sort할 필요가 없다.
map의 value에 pii를 넣고, .first는 처음 나온 index, .second는 마지막으로 나온 index를 넣고
[m[a] == null || m[b] == null || m[a].first > m[b].second] (시작 정류장의 index가 도착 정류장의 index보다 더 빨라야만 한다)인 경우에 no, 나머지는 true로 해 버리면 된다.
나는 vector sort 후 upper bound를 했는데, m[a].first보다 크기만 하면 되는 거니까 최댓값으로 갱신하면 되는 것이었다.
string yes = "YES\n", no = "NO\n"; void solve(){ int n, k; cin>>n>>k; map<int, vector<int>> m; // m[i] : station i가 있는 index vector int station; for(int i = 0; i<n; i++){ cin>>station; m[station].push_back(i); } for(auto &[key, value] : m){ sort(value.begin(), value.end(), less<int>()); } int a, b; // a : 시작, b : 도착 string result; for(int i = 0; i<k; i++){ cin>>a>>b; if(m[a].size() == 0 || m[b].size() == 0){ result = no; } else if(upper_bound(m[b].begin(), m[b].end(), m[a][0]) == m[b].end()){ result = no; } else result = yes; cout<<result; } // nlogn 이하 // 지금은 map 썼는데, 좌표 압축을 써야 할지도. 아마 이게 맞는듯? }
D번
greedy 문제. 현재 cost를 계산하고 cost가 높은 것부터 빼면 된다.
bool cmp(pii &a, pii &b){ if(a.first == b.first) return a.second < b.second; return a.first > b.first; } void solve(){ string w; cin>>w; int p; cin>>p; int total_p = 0; vector<pii> arr(w.length()); // .first : alphabet value, .second : index for(int i = 0; i<w.length(); i++){ arr[i] = {w[i] - 'a' + 1, i}; total_p += w[i] - 'a' + 1; } sort(arr.begin(), arr.end(), cmp); vector<bool> isDeleted(w.length(), false); for(pii &elem : arr){ if(total_p <= p) break; total_p -= elem.first; isDeleted[elem.second] = true; } string result = ""; for(int i = 0; i<w.length(); i++){ if(!isDeleted[i]) result += w[i]; } cout<<result<<'\n'; }
Upsolving
E번
처음에는 다음과 같이, A에 넣을 수 있으면 넣고, A에 넣을 수 없다면 B에 넣고, 그것도 안 된다면 못 넣는 것으로 간주했다. 그러나 뭔가 반례가 있나 보다.
string no = "NO\n", yes = "YES\n"; bool insertable(pii& domino, vector<bool>& isUsed){ if(domino.first == domino.second) return false; else if(!isUsed[domino.first] && !isUsed[domino.second]) return true; else return false; } void solve(){ int n; cin>>n; // 짝수 vector<pii> dominos(n); // 1~n까지 수를 포함함 for(pii &domino : dominos){ cin>>domino.first>>domino.second; domino.first--; domino.second--; } // 한쪽에 최대한 넣을 수 있을 만큼 넣고 vector<bool> isUsedA(n, false), isUsedB(n, false); for(pii &domino : dominos){ if(insertable(domino, isUsedA)){ isUsedA[domino.first] = isUsedA[domino.second] = true; } else if(insertable(domino, isUsedB)){ isUsedB[domino.first] = isUsedB[domino.second] = true; } else{ cout<<no; return; } } cout<<yes; // 이게 왜 동작을 안하는지는 잘 모르겠는데, // bipartite 검증이라는 생각이 팍 든다. 모든 subgraph가 bipartite then true, else false 감이다. }
그러고 제출 10분 전에 graph 접근인가..? 싶어서 조금 끄적끄적 했는데, vertex를 1부터 n까지 두고, 각 domino를 edge로 생각하는 것이다. 만약 domino를 정확하게 2개로 나눌 수 있다면 모든 edge color가 달라야 한다, 는 생각이 팍 들어서 bipartite graph 검증이라는 문제 아닐까? 라는 접근을 떠올렸다. bipartite 검증 자체는 쉽다.
string no = "NO\n", yes = "YES\n"; bool isBipartite(int start_node, vector<vector<int>>& edges, vector<int>& colors){ queue<int> q; // vertex number colors[start_node] = 1; q.push(start_node); while(!q.empty()){ int cur = q.front(); q.pop(); for(int adj : edges[cur]){ if(colors[adj] == colors[cur]) return false; if(colors[adj] == 0){ // unvisited colors[adj] = 3 - colors[cur]; // red then black, black then red q.push(adj); } } } return true; } void solve(){ int n; cin>>n; // 짝수 vector<vector<int>> edges(n); vector<int> colors(n, 0); // 0 : nothing, 1 : red, 2 : black int from, to; bool fault = false; for(int i = 0; i<n; i++){ cin>>from>>to; from--; to--; edges[from].push_back(to); edges[to].push_back(from); if(edges[from].size() > 2 || edges[to].size() > 2){ ////////////// 여기 fault = true; } } if(fault){ cout<<no; return; } for(int i = 0; i<n; i++){ if(colors[i] == 0){ if(!isBipartite(i, edges, colors)){ cout<<no; return; } } } cout<<yes; return; // bipartite 검증이라는 생각이 팍 든다. 모든 subgraph가 bipartite then true, else false 감이다. }
그리고 아래 그림과 같이 반례가 하나 존재하는데, 이렇게 주어지는 경우는 bipartite임에도 불구하고 domino를 나눌 수 없다. 따라서 ////////여기 라고 적힌 부분처럼 작성한다.
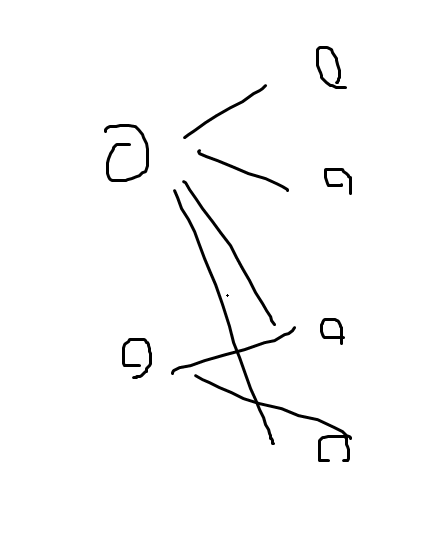
F번
이것도 거의 접근 다 한 것 같은데... 일단 내가 처음 했던 접근은 multiset a에 있는 모든 수를 홀수가 될 때까지 나누는 것이다. 이렇게 나누는 근거는 operation이 *2, /2이기 때문에 a가 짝수인 경우 b의 element를 /2해서 맞춰줄 수 있기 때문이다. - 여기까지 접근했었다.
추가로, 해설지 보니까 이렇게 하면 multiset a에 있는 모든 수들은 홀수가 되기 때문에 multiset b의 element에 operation *2를 사용하면 짝수가 되고, 따라서 operation *2는 금지된다.
+, a, b를 multiset이나 map에 담아넣어서 b element가 a에 없다면 /2하고 b에 다시 추가, a에 있다면 빼는 식으로 전개하면 된다.(이걸 못했네..) 이렇게 하면 O(nlogn)으로 풀린다. 너무 아쉽다!
그리고 multiset 사용시, multiset.erase(value)를 해 버리면 multiset에 있는 value 값을 가진 모든 element를 지우기 때문에 iterator로 지워야 한다.
void solve(){ int n; cin>>n; int ai, bi; multiset<int> a, b; for(int i = 0; i<n; i++){ cin>>ai; while(ai % 2 == 0) ai /= 2; a.insert(ai); } for(int i = 0; i<n; i++){ cin>>bi; while(bi % 2 == 0) bi /= 2; b.insert(bi); } // 나눌 수 있는 최대로 나누기 while(!b.empty()){ int belem = *b.begin(); if(a.find(belem) == a.end()){ // not found in a if(belem == 0) break; // 만약 b가 0이라면 못 찾은 것 b.erase(b.find(belem)); b.insert(belem/2); } else{ // found b.erase(b.find(belem)); a.erase(a.find(belem)); } // multiset 특 : erase(value) 하면 value값 전부 지워짐. 따라서 iter로 지워야 함 } cout<<(b.empty()?"YES\n":"NO\n"); }
G1, G2
깨부
'PS > PS Log' 카테고리의 다른 글
| 22.08.14. 풀었던 문제들 (0) | 2022.08.15 |
|---|---|
| 22.08.13. 풀었던 문제들 (0) | 2022.08.13 |
| 22.08.11. 풀었던 문제들 (0) | 2022.08.13 |
| 22.08.10. 풀었던 문제들 (0) | 2022.08.10 |
| 22.08.09. 풀었던 문제들 (0) | 2022.08.09 |
